Triangulation (geometry)

Related topics include Point set triangulation and Polygon triangulation.

In advanced geometry, in the most general meaning, triangulation is a subdivision of a geometric object into simplices. In particular, in the plane it is a subdivision into triangles, hence the name.

Different branches of geometry use slightly differing definitions of the term.

A triangulation T of 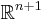$\mathbb{R}^{n%2B1}$ is a subdivision of 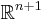$\mathbb{R}^{n%2B1}$ into (n + 1)-dimensional simplices such that:

any two simplices in T intersect in a common face or not at all;
any bounded set in 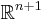$\mathbb{R}^{n%2B1}$ intersects only finitely many simplices in T.

A point set triangulation, i.e., a triangulation of a discrete set of points 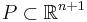$P\subset\mathbb{R}^{n%2B1}$ is a subdivision of the convex hull of the points into simplices such that any two simplices intersect in a common face or not at all and the set of points that are vertices of the subdividing simplices coincides with $P$ . The Delaunay triangulation is a famous triangulation of a set of points where the circum-hypersphere of each simplex contains none of the points.

External links

Weisstein, Eric W., "Simplicial complex" from MathWorld.
Weisstein, Eric W., "Triangulation" from MathWorld.

Triangulation (geometry)

See also

External links